একটি ভার্কল গাছ একটি প্রতিশ্রুতিমূলক স্কিম যা একটি মার্কেল গাছের মতো কাজ করে, তবে এর অনেক ছোট সাক্ষী রয়েছে। এটি একটি ভেক্টর প্রতিশ্রুতি দিয়ে একটি Merkle গাছের হ্যাশগুলিকে প্রতিস্থাপন করে কাজ করে, যা বিস্তৃত শাখার কারণগুলিকে আরও দক্ষ করে তোলে৷
পোস্টে প্রতিক্রিয়ার জন্য কেভাউন্ড্রে ওয়েডারবার্নকে ধন্যবাদ।
ভার্কল গাছ কিভাবে কাজ করে তার বিস্তারিত জানার জন্য, দেখুন:
এই পোস্টের উদ্দেশ্য হল খসড়া ভার্কল ট্রি EIP এর কংক্রিট বিন্যাস ব্যাখ্যা করা। এটি ক্লায়েন্ট ডেভেলপারদের লক্ষ্য করে যারা ভার্কল ট্রি বাস্তবায়ন করতে চান এবং EIP এর গভীরে যাওয়ার আগে একটি পরিচিতি খুঁজছেন।
ভার্কল গাছ গাছের গঠনে অনেক পরিবর্তন আনে। সবচেয়ে উল্লেখযোগ্য পরিবর্তনগুলি হল:
ভার্কল গাছের ভেক্টর প্রতিশ্রুতি স্কিম হিসাবে, আমরা পেডারসেন প্রতিশ্রুতি ব্যবহার করি . Pedersen প্রতিশ্রুতি উপবৃত্তাকার বক্ররেখা উপর ভিত্তি করে. পেডারসেনের প্রতিশ্রুতিগুলির একটি ভূমিকার জন্য এবং অভ্যন্তরীণ পণ্য আর্গুমেন্টগুলি ব্যবহার করে বহুপদ বা ভেক্টর প্রতিশ্রুতি হিসাবে কীভাবে ব্যবহার করা যায়, এখানে দেখুন৷
আমরা যে বক্ররেখাটি ব্যবহার করছি তা হল ব্যান্ডার্সন্যাচ। এই বক্ররেখাটি বেছে নেওয়া হয়েছে কারণ এটি কার্যকরী, এবং এছাড়াও এটি BLS12_381-এর দক্ষ SNARK-কে ভবিষ্যতে ভার্কল ট্রি সম্পর্কে যুক্তি দিতে অনুমতি দেবে৷ এটি রোলআপের জন্য উপযোগী হতে পারে এবং সেইসাথে একটি আপগ্রেডের অনুমতি দিতে পারে যেখানে সমস্ত সাক্ষীকে একটি SNARK-এ সংকুচিত করা যেতে পারে যা ব্যবহারিক হয়ে গেলে, আর কোন প্রতিশ্রুতি আপডেটের প্রয়োজন ছাড়াই৷
ব্যান্ডার্সন্যাচের কার্ভ অর্ডার/স্কেলার ফিল্ড সাইজ হল p =13108968793781547619861935127046491459309155893440570251786403306729687678> , যা একটি 253 বিট প্রাইম। এর ফলস্বরূপ, আমরা কেবলমাত্র সর্বাধিক 252 বিটের বিট স্ট্রিংগুলিতে নিরাপদে প্রতিশ্রুতিবদ্ধ হতে পারি, অন্যথায় ক্ষেত্রটি উপচে পড়ে। আমরা ভার্কল ট্রির জন্য 256 এর একটি ব্রাঞ্চিং ফ্যাক্টর (প্রস্থ) বেছে নিয়েছি, যার অর্থ প্রতিটি প্রতিশ্রুতি প্রতিটি 252 বিটের 256 মান পর্যন্ত কমিট করতে পারে (বা সুনির্দিষ্টভাবে বলতে গেলে, p - 1 পর্যন্ত পূর্ণসংখ্যা ) আমরা এটি কমিট(v₀, v₁, …, v₂₅₅) হিসাবে লিখি v তালিকায় প্রতিশ্রুতিবদ্ধ করতে দৈর্ঘ্য 256।
ভার্কেল ট্রি ইআইপি-র ডিজাইন লক্ষ্যগুলির মধ্যে একটি হল প্রতিবেশী অবস্থানগুলিতে অ্যাক্সেস করা (যেমন প্রায় একই ঠিকানা বা প্রতিবেশী কোড খণ্ডগুলির সাথে স্টোরেজ) অ্যাক্সেসের জন্য সস্তা। এটি করার জন্য, একটি কী একটি স্টেম নিয়ে গঠিত 31 বাইট এবং একটি প্রত্যয় মোট 32 বাইটের জন্য এক বাইট। মূল স্কিমটি এমনভাবে ডিজাইন করা হয়েছে যাতে "ক্লোজ" স্টোরেজ অবস্থানগুলি একই স্টেম এবং একটি ভিন্ন প্রত্যয়ের সাথে ম্যাপ করা হয়। বিস্তারিত জানার জন্য অনুগ্রহ করে EIP খসড়া দেখুন।
ভার্কল গাছ নিজেই তখন দুই ধরনের নোডের সমন্বয়ে গঠিত:
একটি এক্সটেনশন নোডের প্রতিশ্রুতি হল একটি 4 উপাদান ভেক্টরের প্রতিশ্রুতি; বাকি পজিশন 0 হবে। এটি হল:
C₁ এবং C₂ হল আরও দুটি প্রতিশ্রুতি যা stem এর সমান স্টেম সহ সমস্ত মানের প্রতি প্রতিশ্রুতিবদ্ধ . আমাদের প্রতিশ্রুতি দেওয়ার কারণ হল যে মানগুলির 32 বাইট রয়েছে, কিন্তু আমরা প্রতি ক্ষেত্রের উপাদানগুলির জন্য শুধুমাত্র 252 বিট সংরক্ষণ করতে পারি। একটি একক প্রতিশ্রুতি এইভাবে 256 মান সঞ্চয় করার জন্য যথেষ্ট হবে না। তাই এর পরিবর্তে C₁ প্রত্যয় 0 থেকে 127-এর মান সঞ্চয় করে এবং C₂ 128 থেকে 255 সঞ্চয় করে, যেখানে ক্ষেত্রের আকারের সাথে মানানসই করার জন্য মানগুলিকে দুই ভাগে ভাগ করা হয় (আমরা পরে এটিতে আসব।)
প্রতিশ্রুতি C₁ এবং C₂ সহ এক্সটেনশনকে "এক্সটেনশন-এন্ড-সফিক্স ট্রি" (সংক্ষেপে EaS) হিসাবে উল্লেখ করা হয়।
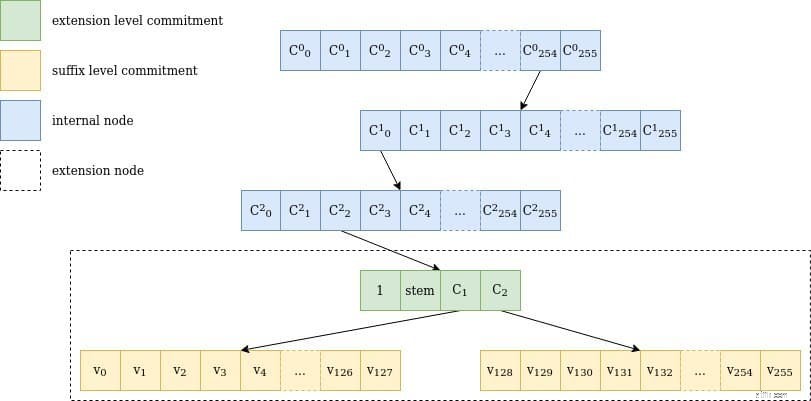চিত্র 1 কী 0xfe0002abcd..ff04 জন্য একটি ভার্কল গাছের মধ্য দিয়ে হাঁটার প্রতিনিধিত্ব :পথটি 3টি অভ্যন্তরীণ নোডের মধ্য দিয়ে যায় যার প্রতিটিতে 256টি শিশু থাকে (254, 0, 2), একটি এক্সটেনশন নোড প্রতিনিধিত্ব করে abcd..ff এবং 04-এর মান সহ দুটি প্রত্যয় গাছের প্রতিশ্রুতি , v₄. মনে রাখবেন যে স্টেম প্রকৃতপক্ষে অভ্যন্তরীণ নোডের মধ্য দিয়ে পথ সহ কী-এর প্রথম 31 বাইট
প্রতিটি এক্সটেনশন এবং প্রত্যয় ট্রি নোডে 256টি মান থাকে। যেহেতু একটি মান 256 বিট প্রশস্ত, এবং আমরা একটি ফিল্ড এলিমেন্টে শুধুমাত্র 252 বিট নিরাপদে সংরক্ষণ করতে পারি, আমরা যদি চেষ্টা করি তাহলে চারটি বিট হারিয়ে যাবে তাই একটি ফিল্ড এলিমেন্টে একটি মান সংরক্ষণ করুন।
এই সমস্যাটি এড়াতে, আমরা 256টি মানের গ্রুপকে 128টি মানের দুটি গ্রুপে বিভক্ত করতে বেছে নিয়েছি। একটি গ্রুপের প্রতিটি 32-বাইট মান দুটি 16-বাইট মানগুলিতে বিভক্ত। সুতরাং একটি মান vᵢ∈ 𝔹₃₂ v⁽ˡᵒʷᵉʳ⁾ᵢ ∈ 𝔹₁₆ এবং v⁽ᵘᵖᵖᵉʳ⁾ᵢ∈ 𝔹₁₆ যেমন যে v⁽ˡᵒʷᵉʳ⁾ᵢ ++ v⁽ᵘᵖᵖᵉʳ⁾ᵢ =vᵢ।
একটি "লিফ মার্কার" যোগ করা হয়েছে v⁽ˡᵒʷᵉʳ⁾ᵢ, এমন একটি পাতার মধ্যে পার্থক্য করতে যা কখনও অ্যাক্সেস করা হয়নি এবং একটি পাতা যা 0s দিয়ে ওভাররাইট করা হয়েছে৷ কোনও মান কখনও ভার্কল গাছ থেকে মুছে যায় না . আসন্ন রাজ্য মেয়াদোত্তীর্ণ স্কিমগুলির জন্য এটি প্রয়োজন। যে মার্কারটি 129 তম বিট এ সেট করা হয়েছে, যেমন V⁽ˡᵒʷᵉʳ ᵐᵒᵈⁱᶠⁱᵉᵈ⁾ᵢ =v⁽ˡᵒʷᵉʳ⁾ᵢ + 2¹²⁸ এর আগে অ্যাক্সেস করা হয়েছে, এবং v⁽ˡᵒʷᵉʳ ᵐᵒᵈⁱᶠⁱᵉᵈ⁾ᵢ =0 যদি Vᵢ অ্যাক্সেস করা হয় না।
দুটি প্রতিশ্রুতি C₁ এবং C₂ তারপর
হিসাবে সংজ্ঞায়িত করা হয়৷
একটি এক্সটেনশন নোডের প্রতিশ্রুতি একটি "এক্সটেনশন মার্কার" দ্বারা গঠিত, যা মাত্র 1 নম্বর, দুটি সাবট্রি অঙ্গীকার C₁ এবং C₂ এবং স্টেম এই এক্সটেনশন নোডের দিকে নিয়ে যাওয়া কীটির।
মার্কেল-প্যাট্রিসিয়া ট্রির এক্সটেনশন নোডের বিপরীতে, যেটিতে শুধুমাত্র কীটির অংশ থাকে যা প্যারেন্ট অভ্যন্তরীণ নোডকে চাইল্ড অভ্যন্তরীণ নোডের সাথে সেতু করে, স্টেমটি সেই বিন্দু পর্যন্ত পুরো কীটিকে ঢেকে রাখে। এর কারণ হল ভার্কল গাছগুলি স্টেটলেস প্রমাণের কথা মাথায় রেখে ডিজাইন করা হয়েছে:যদি একটি নতুন কী ঢোকানো হয় যা এক্সটেনশনটিকে দুটিতে "বিভক্ত" করে, তবে বড় ভাইবোনকে আপডেট করার প্রয়োজন নেই, যা একটি ছোট প্রমাণের অনুমতি দেয়৷
অভ্যন্তরীণ নোডগুলিতে তাদের প্রতিশ্রুতিগুলির জন্য সহজ গণনা পদ্ধতি রয়েছে:নোডটিকে 256টি মানের ভেক্টর হিসাবে দেখা হয়, যা তাদের 256টি উপবৃক্ষের প্রতিটির মূল প্রতিশ্রুতি (ক্ষেত্রের প্রতিনিধিত্ব)। একটি খালি সাবট্রির জন্য প্রতিশ্রুতি হল 0৷ যদি সাবট্রি খালি না থাকে, তাহলে অভ্যন্তরীণ নোডের জন্য প্রতিশ্রুতি হল
যেখানে Cᵢ হল অভ্যন্তরীণ নোডের সন্তান, এবং 0 যদি একটি শিশু খালি থাকে।
চিত্র 2 হল গাছের মধ্যে একটি নতুন মান ঢোকানোর প্রক্রিয়ার একটি দৃষ্টান্ত, যেটি আকর্ষণীয় হয়ে ওঠে যখন ডালপালা কয়েকটি প্রাথমিক বাইটে সংঘর্ষ হয়।
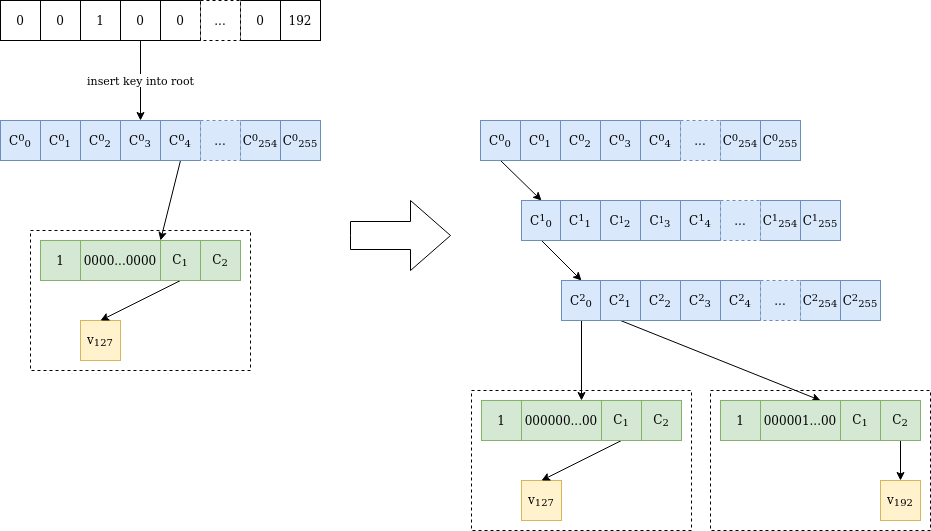
চিত্র 2 মান v₁₉₂ অবস্থানে ঢোকানো হয়েছে 0000010000...0000 অবস্থান 0000000000...0000 এ শুধুমাত্র v₁₂₇ মান ধারণকারী একটি ভার্কল গাছে . যেহেতু তৃতীয় বাইটে ডালপালা আলাদা, ভিন্ন বাইট পর্যন্ত দুটি অভ্যন্তরীণ নোড যোগ করা হয়। তারপরে একটি সম্পূর্ণ 31-বাইট স্টেম সহ আরেকটি "এক্সটেনশন-এন্ড-সফিক্স" গাছ ঢোকানো হয়। প্রাথমিক নোডটি স্পর্শ করা হয়নি, এবং সন্নিবেশের আগে C²₀-এর মান C⁰₀-এর মতোই রয়েছে।
ভার্কল গাছের গঠন অগভীর গাছের জন্য তৈরি করে, যা সঞ্চিত ডেটার পরিমাণ হ্রাস করে। এর আসল শক্তি, তবে, ছোট প্রমাণ, অর্থাৎ সাক্ষী তৈরি করার ক্ষমতা থেকে আসে। এটি পরবর্তী নিবন্ধে ব্যাখ্যা করা হবে।
